(image from https://www.tribuneindia.com/2014/20141116/spectrum/motor.htm)
Let’s talk about body language.
 A key property of body language is that it is almost always unconscious to both giver and receiver.
A key property of body language is that it is almost always unconscious to both giver and receiver.
Image from: https://talbotspy.org/but-his-tail-was-wagging-understanding-dog-body-language-part-1/
This is not a problem in itself – in fact, it’s actually really good that body language happens mostly unconsciously. Body language is necessarily unconscious. The flood of signals from a talking body is vast, high-bandwidth, high-rate, and highly-parallel. It must bypass the higher-brain in order to do its work. The higher brain is too busy making decisions and trying to be rational to be bothered with such things.
The problem with the backchannel nature of body language is that it is often in competition with explicit, linear verbal language, which is a pushy tyrant. There are too many pushy tyrants in the tech industry that are poor at social signaling. Body language tends to be relegated to a lower priority in many areas of digital technology, including the design of software interfaces, productivity tools, kitchen appliances…and cars. This is just one symptom of the lack of diversity in the tech industry.
High tech culture is obsessed with metrics; seeking to measure as much as possible, to be data-driven, to have tangible results and ways of measuring success. This obsession with data is a mistake. Tossing out what can’t be measured or converted into data is a very big mistake. And the digitally-designed world we live in suffers as a result. Let me try to explain what I mean by all this….
A computer on wheels


The automobile was invented in the industrial age – an age defined by energy, force, mechanics, chemistry, electricity, and physicality.
We are now fumbling through the information age.
Apple Inc. has managed to reduce the thickness of laptop computers – they have become so thin that you can cut steak with them. But it should come as no surprise that the surface areas of laptop screens and keyboards have not been reduced, compared to the degree that computer chips have been miniaturized. There is a simple reason for this: human eyes and hands are still the same size. This will never change.
The same applies to communication. The more digital our machines become, the more we have to communicate with them, and they, in turn, have to communicate with us.
 An old-fashioned industrial-age car comes with natural affordances: communication happens simply as a result of the physical nature of knobs, wheels, wires, engine sounds, torques, and forces. There are many sensory stimuli that the driver sees, feels, hears and smells – and often they are unconscious to the driver – or just above the level of consciousness.
An old-fashioned industrial-age car comes with natural affordances: communication happens simply as a result of the physical nature of knobs, wheels, wires, engine sounds, torques, and forces. There are many sensory stimuli that the driver sees, feels, hears and smells – and often they are unconscious to the driver – or just above the level of consciousness.
Driving is a very different experience now. It is turning into a video game…a simulation. There is a disconnect between driver and car that seems to be growing wider.
That’s not necessarily a bad thing. But here’s the problem:
Body language between driver and car has become an arbitrary plaything, mediated by cockeyed displays and confusing controls. It is up to the whims of user interface designers – too many of whom have their heads up their asses. Idiots who call themselves designers live under the illusion that they can invent visual language on the fly and shove it into our long-lived lives, expecting their clever interfaces to fall naturally into use.
Or maybe they don’t actually think this – but don’t care anyway, because they are paid well. I’m not sure which is worse.

According to Matt Bubbers:
There’s nothing wrong with the volume knob. It does not need reinvention, nor disruption, nor innovation. The volume knob is perfect the way it is. Or, rather, the way it was.
Get into a new car in 2018 and you’re faced with a multitude of complicated ways to adjust the stereo volume: buttons or dials on the steering wheel, voice commands that rarely work, fiddly non-buttons on the centre panel, touchscreens that take your eyes off the road, even gesture controls that make you wave your hand as if you’re conducting a symphony.
Cars are too complicated. The volume knob is indicative of the problem. Call it feature bloat or mission creep: Cars are trying to do more, but they’re not doing it all well. These infotainment features can be distracting, therefore dangerous, and they cost money.
A new generation of digital designer is out of touch with nature. It is infuriating, because here we are, fumbling to bake a cake, turn on the AC, or change a channel on the TV: “Now, which of these 2,458 buttons on this TV remote do I need to press in order to change the channel?…”
“Oh shit – no wonder I’m confused: this is the remote control for the gas fireplace! Is that why it’s so hot in here?”
Driving under the influence of icons
Britania Rescue, a firm providing a breakdown service in England, conducted a survey, interviewing over 2000 drivers. The revelations are quite startling. It revealed that more than 52 per cent of drivers cannot correctly identify 16 of the most common symbols.

Interpreting a bunch of unfamiliar icons invented by out-of-touch dweebs is not how we should be interacting with our technology – especially as technology sinks deeper into our lives.
Just this morning, my 87-year-old mother and I spent about a half-hour trying to figure out how to set my sister’s high-tech oven to bake. To make matters worse, my mother, who is visually-impaired, can’t even feel the controls – the entire interface consists of a dim visual glow behind slick glass. We eventually had to read a manual. WE HAD TO READ A FUCKING MANUAL TO FIGURE OUT HOW TO TURN ON AN OVEN. How long must this insanity go on?
A car’s manual should be the car itself

Dan Carney, in the article, Complex car controls equal confused drivers, quotes Consumer Reports: “You shouldn’t have to read the owner’s manual to figure out how to use the shifter.”
He says, “The BMW iDrive had a controller for functions like the radio and air conditioning that was so baffling that it forced drivers to take their eyes off the road.”
My Prius experience
 My first experience with a Prius was not pleasant. Now, I am not expecting many of you to agree with my criticism, and I know that there are many happy Prius owners, who claim that you can just ignore the geeky stuff if you don’t like it.
My first experience with a Prius was not pleasant. Now, I am not expecting many of you to agree with my criticism, and I know that there are many happy Prius owners, who claim that you can just ignore the geeky stuff if you don’t like it.
I don’t like it, and I can’t ignore it.
I have found that most people have a higher tolerance for figuring-out technology than I. It’s not for lack intelligence or education; it’s more that I am impatient with stupid design. It makes me irate, because these fumblings are entirely unnecessary.
We all suffer because of the whims of irresponsible designers, supposedly working in teams which include human factors engineers and ergonomics engineers, whom I assume are asleep on the job.
I place the blame for my impatience squarely on Donald Norman, whose book, “The Design of Everyday Things” implored readers to stop blaming themselves for their constant fumbling with technology. The source of the problem is irresponsible design. He converted me profoundly. And now I am a tech curmudgeon. Thanks Don.
I once had to borrow a friend’s Prius because my Honda Fit was in the shop. I liked the energy-saving aspects and the overall comfort, but the dashboard was unfamiliar. My hippocampi threw up their hands in despair. What’s worse: after parking the car in a parking lot, I put the key in my pocket and decided to check the doors to make sure they were locked. The doors were not locking. Why? I tried locking the doors many times but every time I walked around to the other side, the opposite door would unlock. I called the owner, and told her that I am not able to lock the car. She said, “Oh – that’s because the doors automatically – and magically – unlock when you walk up to them. Smart, eh?”
Hello? Discoverability?
Thank you Prius for not telling me about your clever trick. You are one step ahead of me! Perhaps I should just stop trying to understand what the fuck you are doing and just bow to your vast intelligence. You win, Prius.
My Honda Fit is relatively simple, compared to many cars these days. But it does things that infuriate me. It decides that I want the back window wipers to turn on when the front wipers are on, and I happen to be backing up. It took my car mechanic to explain the non-brilliance of this behavior. Thanks Honda for taking away my choice in the matter. My car also decides to turn on the interior light at night after I have parked the car. I have to wait a long time for the light to go out. My car knows how long. I am not privy to this duration. What if I don’t want strangers to see me – because I’d like to finish picking my nose before getting out?
Whether or not strangers can see me picking my nose is no longer my choice. My car has made this decision for me. Sure: I could reach up to the ceiling and turn off the light – but then I will forget to turn it on again when I actually need it. This never used to be so complicated.
Smart = dumb
I have come to the conclusion that a car without any computers is neither smart nor dumb. It has no brain and so it cannot even try to be intelligent. On the other hand, if a car has computational processing then it has an opportunity to be either smart or dumb. Most cars these days are poor communicators, I call them dumb.

The decider
Another gripe: sometimes my door locks when I’m driving, and then I have to unlock it to get out – but not always. There is no rhyme or reason (that I am aware of) for when and why this happens. Yes…I know – some of you will probably offer to enlighten me with a comment. But the fact that this has to be learned in the first place is what bugs me. I would prefer one of two things: (1) My car makes it apparent to me why it is making decisions for me, or (2) it stays out of the way and lets me be the decision-maker.
Am I old-fashioned? If wanting to be in charge of basic things like locking doors and turning on lights makes me old-fashioned, then…yes, I’m old-fashioned.

(image from http://www.thehogring.com/2013/07/31/10-most-ridiculous-dashboards-of-all-time/
Confessions of a MIT luddite
People confuse me for a techy because of my degree. And then they are shocked at how critical I am of technology. The truth is that I am a design nerd rather than a computer nerd. I have nothing against information technology – after all, I write software – and love it. I just want the technology that I rely on to be better at communicating. For example: why do gas pumps still have a one-word vocabulary? ….
Beep.
Okay, I’m a neo-luddite. There, I said it. And I will remain a neo-luddite as long as the tech industry continues to ignore a billion years of evolution, which gave us – and the rest of the living world – the means to generate signals and interpret signals – the body language of the biosphere that keeps the living world buzzing along.
This natural flow of communication among organisms is a wonderful thing to behold. It happens on a level of sophistication that makes ovens and VCR’s look like retardation in a box.
But then again, the evolution of information technology is extremely short compared to the evolution of natural language, which has kept the social ecosystems of Homo Sapiens running for a very long time.
Perhaps I am thrashing in the midst of the Singularity, and I should just give up – because that’s what you do in the Singularity.
But I would still like to understand what the future of communication will look like. This is especially important as more and more communication is done between people and machines. At the moment, I am still a little hesitant to call it “communication”.


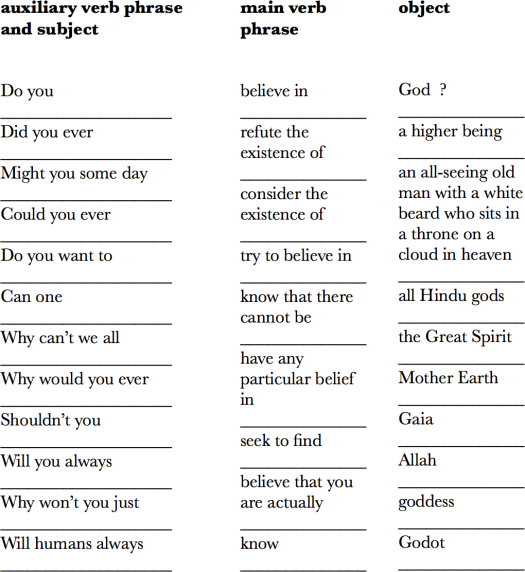

 To be fair, it is possible that given a particular situation, the first sentence might make sense. Consider: “The pig is hungry and usually gets fed at 5:30pm,
To be fair, it is possible that given a particular situation, the first sentence might make sense. Consider: “The pig is hungry and usually gets fed at 5:30pm, 
 Remember Nietzsche’s famous announcement, “
Remember Nietzsche’s famous announcement, “ My book,
My book, 
 A key property of body language is that it is almost always unconscious to both giver and receiver.
A key property of body language is that it is almost always unconscious to both giver and receiver.

 An old-fashioned industrial-age car comes with natural affordances: communication happens simply as a result of the physical nature of knobs, wheels, wires, engine sounds, torques, and forces. There are many sensory stimuli that the driver sees, feels, hears and smells – and often they are unconscious to the driver – or just above the level of consciousness.
An old-fashioned industrial-age car comes with natural affordances: communication happens simply as a result of the physical nature of knobs, wheels, wires, engine sounds, torques, and forces. There are many sensory stimuli that the driver sees, feels, hears and smells – and often they are unconscious to the driver – or just above the level of consciousness.


 My first experience with a Prius was not pleasant. Now, I am not expecting many of you to agree with my criticism, and I know that there are many happy Prius owners, who claim that you can just ignore the geeky stuff if you don’t like it.
My first experience with a Prius was not pleasant. Now, I am not expecting many of you to agree with my criticism, and I know that there are many happy Prius owners, who claim that you can just ignore the geeky stuff if you don’t like it.